Hukum Bernoulli Dan Studi Kasus

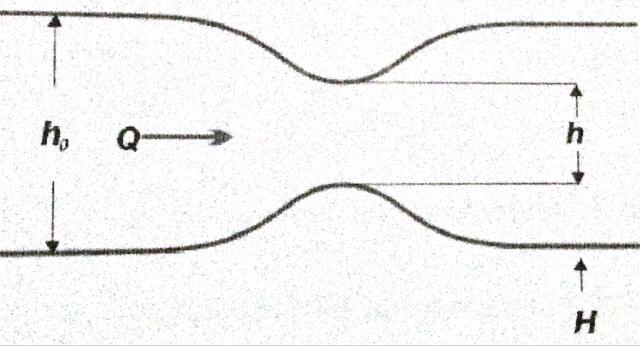
Misalkan terdapat sebuah saluran dengan penampang sesuai dengan Gambar dibawah.

 

Berdasarkan hukum Bernoulli, maka diperoleh persamaan berikut:

$$\begin{array}{}\frac{Q^2}{2g{b}^2{h}_0^2}+h_0=\frac{Q^2}{2g{b}^2{h}^2}+h+\end{array}$$

Persamaan tersebut dapat dilakukan transformasi menjadi persamaan berikut:

$$\begin{array}{}f\left(h\right)=h^3+\left(H-\frac{Q^2}{2g{b}^2{h}_0^2}-h_0\right)h^2+\frac{Q^2}{2g{b}^2}=0\end{array}$$

Data-data terkait saluran tersebut adalah sebagai berikut:

• $Q=1,2\frac{m^3}{det}$ = volume aliran fluida tiap satuan waktu
• $g=9,81\frac{m}{s^2}$
• =percepatan gravitasi
• $b=1,8m$
• =lebar pipa
• $h_0=0,6m$
• =ketinggian air maksimum
• $H=0,075m$
• =tinggi pelebaran pipa
• $h$

Kita dapat menggunakan pendekatan numerik untuk menentukan $h$

. Pada studi kasus ini tidak dijelaskan lokasi dimana akar penyelesaian berada, sehingga metode terbuka seperti Secant cukup sesuai untuk menyelesaikannya:

Berikut adalah persamaan yang baru setelah seluruh data dimasukkan kedalam tiap variabelnya:

$$f\left(h\right)=h^3+\left(0,075-\frac{1,2^2}{2\times 9,81\times 1,8^2\times 0,6^2}-0,6\right)h^2+\frac{1,2^2}{2\times 9,81\times 1,8^2}=0$$

Untuk penyelesaiannya penulis akan memberikan tebakan awal nilai $h=h_0=0,6$

. Berikut adalah sintaks penyelesaian menggunakan metode secant:

f <- function(h){
  (h^3) + ((0.075-((1.2^2)/(2*9.81*(1.8^2)*(0.6^2))))*h^2)+ (1.2^2/(2*9.81*(1.8^2)))
}
root_secant(f, 0.6)

## $`function`
## function (h) 
## {
##     (h^3) + ((0.075 - ((1.2^2)/(2 * 9.81 * (1.8^2) * (0.6^2)))) * 
##         h^2) + (1.2^2/(2 * 9.81 * (1.8^2)))
## }
## <bytecode: 0x000000001d1483f0>
## 
## $root
## [1] -0.287
## 
## $iter
## [1] 26

Berdasarkan hasil perhitungan diperoleh nilai $h=-0,2870309$

atau ketinggian air sekitar $0,3m$ dengan jumlah iterasi sebanyak $26$

kali.

Pembaca dapat mencoba menggunakan metode lain seperti metode tertutup. Untuk dapat melakukannya, pembaca perlu memperoleh rentang lokasi akar persamaan tersebut berada menggunakan metode tabel.

 

STUDI KASUS 

Penerapan penyelesaian sistem persamaan non-linier banyak dijumpai dalam berbagai kasus di bidang lingkungan. Pada bagian ini penulis tidak akan menjelaskan seluruhnya. Penulis hanya akan menjelaskan penerapannya pada sebuah persamaan yaitu Hukum Bernoulli.